The reduced Enigma
Harold Thimbleby*
Gresham Professor of Geometry
Gresham College
Barnard's Inn Hall
Holborn
LONDON, EC1N 2HH
Abstract
This article describes a simplified cryptographic machine, based closely on the World War II Enigma. This 'reduced Enigma' exposes some of the design flaws of the original Enigma in a new way. Had the Axis powers built a reduced Enigma, the outcome of the war might have been different.
A fully working reduced Enigma has been used very successfully in numerous public lectures, in school talks, and in university seminars. Hands-on demonstrations of the reduced Enigma dramatically brings alive ideas about design, codes, permutations and groups. As a working trapdoor function, the reduced Enigma also provides an unusually clear introduction to public key cryptography. This article provides background information, lecture suggestions, and details for building it.
Keywords
Education, Enigma, Public Understanding of Cryptography, "reduced Enigma"
Introduction
Cryptography is a fascinating subject. The paradoxical concept of "sharing secrets" has a natural appeal, and can be used as a motivation to discuss history, mathematics and computer science, or to help motivate many concepts such as key distribution, public key cryptography and digital signatures. This paper describes a simple cryptographic machine, closely based on the World War II Enigma: the machine has been used very successfully in lectures, both to public and school audiences, and to researchers. Design details for a simplified Engima are given, as well as relevant historical and technical context, particularly as highlighted through the simplified design. This paper, then, should be of equal interest to readers interested in cryptography and to lecturers who wish to communicate the ideas clearly, particularly with hands-on participation.
Any good lecture provides ideas that at different points draw the attention of different members of the audience. The Enigma provides an endless source of historical interest, mathematical interest, human factors interest, and so on. It is highly suitable for mixed audiences, typified by grandparents bringing along enthusiastic grandchildren! Likewise, but due to limitations of space rather than time, this paper, too, raises tantalising issues (e.g., Where do some of the numbers come from? What about different versions of the Enigma? What did people, on both sides, learn as the war progressed?) and numerous fascinating potential discursions (e.g., What did Alan Turing contribute? How do we do things better today? What about public keys?) that will stimulate the reader --- or an audience --- into unlimited further activity and reflection. Elsewhere we have discussed how to introduce the underlying cryptographic concepts to audiences of any age or skill, from school children to postgraduate specialists: see Bell et al., 2002.
However, the main point for the present that is conveyed, and that should be conveyed forcibly to all programmers and system developers, is that complex systems --- particularly ones involving any interaction or human element --- are hard to design to be effective and reliable under the pressures of real use, and one should first build simplified systems to fully understand the principles. In an hour's typical lecture, the reduced Enigma can illustrate dramatic weaknesses in the real Enigma.
Mechanical devices are ideal for lectures. Unlike computer programs, you can see how they work, and using them allows participants to attempt more interesting activities than can be done purely manually. With cryptography, we have the added advantage that for an exciting and important period of history, the real devices in life-and-death use were mechanical too. Alfred Scherbius was one of many people in the early twentieth century to patent the basic idea of a mechanical or electromechanical code machine based on rotors. There were many designs and developments, but the most widely-known of these devices was the Enigma. The Enigma was used extensively by the Germans during the Second World War.
Original WWII Enigmas are now valuable antiques, and rebuilding an accurate Enigma is a complex job and one that anyway creates a code that is hard to explain in lectures. Yet in principle, an Enigma is ideal for explaining important concepts, such as key distribution problems, since it is easy enough to change keys and, of course, codes using any key work automatically.
What, then, is the simplest Enigma that can be made?

Figure 1. A German army Enigma in use. Here, pressing S lights up N. The three rotors are just visible under the cover at the top; the plug board is partly covered at the bottom.[1]

Figure 2. Close up of the three rotors. A row of lamps and some of the internal wiring is visible, as well as the switch connections. The rotors of this Army Enigma are set numerically, rather than by using letters. This would help ensure that settings were chosen randomly.

Figure 3. Close up of the Enigma plugboard, showing 9 connections. Note that the plugs and sockets are symmetric and can be inserted incorrectly.
What is the simplest Enigma?
Scherbius's Enigma had a 26 button keyboard (with no space button) and 26 corresponding light bulbs. Briefly, a plugboard and a set of rotors mess up the wiring, so that as buttons are pressed one of the 26 light bulbs come on in turn, but not in any obvious order. The plugboard settings and initial rotor settings represent the key, and another Enigma with the same settings (and internal construction) can decode the message. There were lots of versions of Enigmas; for example the pre-war commercial ones did not have a plugboard. During the war, the Enigma and the procedures for using were under continual development; although the Germans were aware of some of the weaknesses we shall describe, no Enigma consolidated the best features of the different versions into a single machine. Rather than consider all the complications and variations, what is the simplest Engima style machine that works?
One might think that the simplest Enigma would have two buttons, labelled in binary as 0 and 1. Its two light bulbs would also be labelled 0 and 1. When an operator types out a binary message, say, 01011001É the lights would perhaps code it as 11001010É This is clearly the simplest scheme inspired by the Enigma. Unfortunately, because of their design, an Engima with only two buttons would have a disastrous property: 0 would always code as 1, and 1 always code as 0 --- hardly a code. The problem arises due to the Enigma's wiring, but is usually explained more simply: no letter can code as itself. This property of the real Enigma was one of its main weaknesses. Had Scherbius made a reduced Enigma first, he would certainly have spotted the problem. Instead he went for 26 letters straight away,[2] and hence disguised the flaw in a layer of complexity. He and other developers fell for the classic trap of making a complication illusoire. Just making codes more complex rarely makes them harder to solve.
We will see below that this problem of the Enigma design is not the only one that a reduced Enigma exposes.
Figure 4 shows an Enigma circuit taken from a German navy manual. It is easiest to follow the wiring from the battery connection + on the right of the diagram. Suppose the Y button is pressed. Current is connected (along the solid wire at the far left) up to the rotors. The three rotors make a 'random' connection through to the reflector, and then back, where the circuit continues in the dashed wire (emerging from the rotors at the top right). The return wire connects (in this case) to the Z button's switch, where it is connected through to the Z lamp. All lamps have a common return to the - (negative) battery connection. So for these rotor positions, if Y is pressed Z lights; and if Z is pressed Y lights.
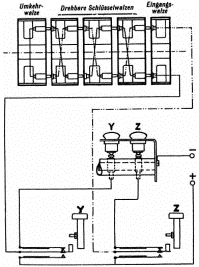
Figure 4. Part of the Enigma circuit, from a German navy manual (from Kahn, 1996b). The diagram shows three rotors at the top, with a reflector on the far left and a contact wheel on the right. In the middle, connected to the - battery terminal, are two (of the 26) lights; at the bottom (connected to the + battery terminal) are two of the key switches.
In actual operation, when a button is pressed the rotors turn, and the particular connection of Y¨Z and Z¨Y might not be repeated for a very long time. Of course if Y and Z are the only buttons, whatever the rotors do in detail, ultimately they cannot connect them any other way than together: which, as we've seen is degenerate. The German navy manual shows a worthless Enigma!
In general the Enigma wiring ensures that no letter can code as itself. The button Y (for example) either connects to the + battery terminal or to the Y lamp. If the Y button is pressed, the Y lamp cannot come on. The same is true for all 26 letters.
This, the Engima's major weakness that no letter can code as itself, facilitates code breaking. If a crib (a suspected word in the plaintext) is slid along a ciphertext, if no letters correspond anywhere, then the crib is a possible decrypt at that point. A good crib might be HEILXHITLER, not least because it was said often, but because it has a pattern of several Hs and Es and Is.
Exploiting this weakness, the British cryptanalysts at Bletchley Park, developing original Polish work, built a machine, the Bombe, that automatically looked for possible decodings. A Bombe would typically find several possible Enigma settings that could possibly code a message containing (say) HEILXHITLER, and a room full of Enigma operators would work through the possible settings systematically until the message was successfully decoded. Using a reduced Enigma helps explain this issue to an audience: it is possible to press one button repeatedly and easily see its corresponding lamp never lights up; on a real Enigma, with 26 lamps flashing, it is impractical to see that a particular lamp never lights.
Why does the Enigma have this property? The simple wiring of the Enigma ensures the code is reciprocal: if Y codes as Z, in the same setting, Z codes as Y. An Enigma set up with the rotas in the same position can be used either to code or decode, and this has practical advantages. In fact, the Enigma could have been designed to be reciprocal without this problem (see Appendix 5), but the problem was not noticed.
Since every letter on the Enigma is coded as another letter, it might seem possible to build a reduced Enigma with three buttons and three lights. Suppose the buttons are XYZ. There are then just two possible codes: {X¨Y, Y¨Z, Z¨X} or {X¨Z, Y¨X, Z¨Y}. But the Enigma was also designed to be reciprocal, so that with the same key settings it could be used to both code and decode messages. With three keys this is not possible. Suppose X codes as Y, then at the same setting Y should code to Z, not to X. Instead, the Enigma should code so that if X codes as Y, then Y codes as X. This reciprocal relation must be true for any pair of letters, and therefore an Enigma must have an even number of letters. The real Enigma had 26 buttons, and in consequence X was used to double up as a space. (There are reciprocal codes with three letters that do work, but which the Enigma wiring can't handle: for instance {X¨Y, Y¨X, ZÇZ} which doesn't work because Z¨Z codes one letter onto itself.)
The simplest Enigma must have 4 buttons and 4 lights.
The reduced Enigma
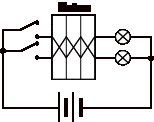
Figure 5 shows the reduced Enigma, which is built in a transparent box so its workings can be seen. Table 1 compares the construction of the reduced Enigma with a typical real Enigma. Table 2 examines the complexities of the reduced Enigma. The essential wiring exactly mirrors the real Enigma's. (Appendix 4 gives the circuit diagrams.)
Instead of rotors, a uniselector is used: unused and second-hand uniselectors can be obtained fairly easily, whereas rotors are hard to make (although during the war they would have been easier to mass produce than wiring-up uniselectors). Uniselectors are electrically operated switches: sending an electrical pulse to their coil changes their connections. Although Enigma rotors changed their connections by mechanical rotation caused by the operator pressing buttons, uniselectors can be used to simulate them, just provided every button has an extra wire to control them. In fact, uniselectors were standard parts of early automatic telephone exchanges, and were also used at Bletchley Park in the "Tunny," a simulator for the German Lorentz code machine.
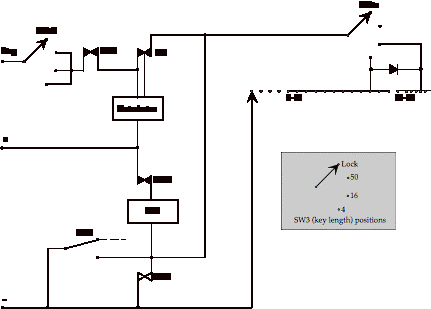
The uniselector in the reduced Enigma can be seen working through the Enigma's transparent cover, and it makes a very satisfying clunky sound as the reduced Enigma is used. The uniselector chosen gives a maximum key length of 50, and it can be wired arbitrarily over the whole length of the key (which rotors cannot be). The reduced Enigma was wired to accurately simulate two 4-way rotors over its first 16 positions, and the remaining 34 positions are random --- though it would have been preferably if the uniselector had had a key length of 64 = 43, which would have allowed simulating three rotors correctly.
|
Real Enigmas |
Reduced Enigma |
|
26 letters and lamps |
4 letters and lamps |
|
26 way plugboard, typically 6 plug cables |
4 way plugboard, 2 plug cables |
|
Switch and lamp wiring |
Identical switch and lamp wiring |
|
Adjustable rotor ring settings |
Rotors cannot be adjusted |
|
Mechanical rotor action |
Electromechanical rotor simulation by uniselector |
|
Control for internal or external power supply, and for bright/dim lamps |
External power only |
|
Swiss K model has external lamp board on ~0.5m cable |
Plugable external lamp board on 6m 'network' cable |
|
12Kg, in wooden box |
2.6Kg, in transparent plastic box |
|
Exchangeable set of 8 rotors |
Fixed
set of 1 or 2 simulated rotors |
Table 1. Enigma and reduced Enigma construction compared.
Reduced Enigma controls
The knobs (bottom left of Figure 5) set the initial rotor positions; pressing the bottom red button resets the reduced Enigma to any of the possible 16 key settings.
The remaining control switch (at the bottom right of Figure 5) selects four choices of key length: both rotors locked (a key length of 1, which is useful for demonstration purposes), one rotor locked (a key length of 4), both rotate (a key length of 16), or --- for fun rather than accurate simulation --- all positions of the uniselector are used, giving, for this reduced Enigma, its maximum key length of 50. (The random wiring of the 34 extra positions was chosen to nearly balance the frequencies of each code.)
The reduced plugboard
The wires from the 4 buttons go to a plugboard, which works just like the Enigma's, to mix up the wiring. A wire plugged between any two sockets swaps the original connections.
The real Enigma has 26 sockets, and hence up to 13 wires. For practical reasons usually only 6 pairs of plugboard connections were made, though the number used increased during the war. The real Enigma used two-pin plugs for the plugboard; the reduced Enigma uses standard jack plugs, which can only be inserted one way round.
Given there are 4 sockets on the reduced Enigma, one might think that there are 4!=24 ways of mixing up its four wires and that there should 'obviously' be 4! reflectors. Similar arguments have been made in the published literature for the real Enigma, where large numbers (26!Å1027) are reported unquestionably.
Drawing diagrams of 26 crossed wires is quite impractical, but the reduced Enigma is small enough for erroneous thinking to be made more obvious. Four sockets and two connector cables can only provide 3 permutations if both cables are always used; but if 0, 1 or 2 cables can used then 10 permutations can be achieved --- but this is still less than half the 24 theoretically possible. The remaining 14 permutations require a different sort of cable: a single cable with three plugs can achieve 8 more permutations (all leaving one socket unchanged), and a single cable with four plugs can achieve the remaining 6 permutations (see Appendix 4). It is interesting that a single cable does better than two: it might also be easier to handle under the pressure or war (or a difficult lecture) --- plugboard wiring mistakes whether or not the operator is under pressure would obviously render the Enigma less than useless. If, for the reduced Enigma, the three different types of connection cables are coloured differently then the codebook table (Appendix 2) can have another entry and all 4! permutations can be used.
The reduced reflector
Out of a hopeful 4! reflectors, by drawing or otherwise, it is easy to see that there are only 3 possible (see Table 2). Furthermore a 'secure' reduced Enigma should only support 2 of these 3 possibilities because two of the reflectors are rotations of each other. (The actual reduced Enigma has wiring for one only.)
Because the reflector connects and hence pairs letters together, the number of reflector wirings is equal to the number of reciprocal simple substitutions. An interesting observation may be made about the real Enigma: since the number of all codes, counting both reciprocal and non-reciprocal codes, is 26! and which is considerably larger (by a factor of ~1014 for n=26; see Table 2), it means that the design decision to make the Enigma reciprocal significantly reduced its security --- a penalty presumably hoped to be offset against the operational convenience. For the reduced Enigma, requiring the reciprocal property reduces the number of codes by a factor of 8 --- which is still a pretty severe tradeoff, since there are only 24«key length different possible substitution codes to start with.
The reduced rotors
In principle there are 4!=24 rotors. But most of the rotors don't achieve anything useful. Many 4 wire rotors are obviously degenerate, a problem which isn't at all obvious when they have 26 wires. For example, the trivial wiring that takes wire 1 to 1, 2¨2, 3¨3 and 4¨4, does nothing different as it is rotated. Indeed, the rotor taking 1¨2, 2¨4, 3¨1 and 4¨3, and many other possible rotors do nothing as they are rotated. They are therefore quite useless. There are then two rotors (e.g., swap 1Ç2, swap 3Ç4) that have only two effectively different positions. This leaves only 4 rotors out of the 24 that do anything useful. Overall, instead of a possible 4! = 24 rotors, only 4 are non-degenerate.
A reduced Enigma with one rotor (carefully chosen from the 4 non-degenerate rotors) would have a key length of 4. One with two rotors should have a key length of 16. Some combinations of rotors give shorter key lengths.
A real Enigma has swappable rotors (to change the wiring) and the rotors rotate. With three rotors, there are 26«26«26 = 15,576 different rotor positions, and the rotors can be put in any order. Later in the war, the rotors were selected from a fixed set of eight, further increasing the number of permutations. The reduced Enigma has the rather more modest arrangement of two (non-degenerate) fixed rotors --- the uniselector is wired to simulate the correct wiring and rotation of two rotors.
A uniselector can easily out-perform the number of permutations of a simple 4-way rotor, and it need have no degenerate connections. Indeed a contemporary uniselector could easily have out-performed a 26 way original Enigma rotor. But small rotors were more practical for actual use, and they would have been easier to wire up. A single 26 letter rotor has only 26 internal wires; in contrast a single 50 way uniselector has already, even for the reduced 4 button Enigma, 100 wires. To make the comparison clearer: the two 4 letter rotors it simulates would have required 8 wires, but just the 16 positions two 4 letter rotors can be in require 48 connections to simulate. Despite these unpromising comparisons, a pair or uniselectors could be wired together, and we would then be comparing 502=2,500 codes (for two uniselectors) or 503=125,000 codes (for three) against a conventional 26 way rotor's improvement to 262=676 or 263=17,576.
Uniselectors are heavier and larger than rotors, and the standard uniselector used in the reduced Enigma requires additional wiring for key setting (to simulate electrically what for a rotor is purely mechanical). Rotors are mechanically easier, which is an important criterion for a device that is intended to be used in action. Building rotors and swapping them around in the field (as keys are changed) mean that a rotor is a lot more convenient than a uniselector.
Since Enigma rotors turn at progressively slower speeds, even for runs of 26 characters two rotors and the reflector are essentially stationary. This makes breaking the code easier, as Alan Turing realised. A set of uniselectors can be wired randomly over the full key length, and need not have this limitation. Thus a uniselector approach to wiring an Enigma would not have this weakness the Enigma had; in fact, the Japanese Purple (so-called by the US) code machine used coupled uniselectors instead of rotors. Appendix 5 shows how the weakness can be avoided with conventional rotors.
|
Property |
Formula n letters, upto p plugboard connections, r rotors, s rotors in use |
Value for reduced Enigma |
|
Number of rotor wirings |
n! |
24, but only 4 are non-degenerate, of which 2 are used on the reduced Enigma. |
|
Number of plugboard permutations, allowing anywhere between i=0 and p connections |
|
10 |
|
Number of reflector wirings |
(equals basic formula for plugboard with p=n/2) |
3, of which 2 are similar. The reduced Enigma has 1 fixed rotor. |
|
Rotor permutations |
|
1 (the reduced Enigma's 2 simulated rotors cannot be changed) |
|
Key length |
|
1, 4, 16 (simulating s=0, 1 or 2 rotors) and 50 (not simulating rotors) |
Table 2.The basic formulae and actual values for the reduced Enigma. A good exercise is to work through these formulae for cases of 6 key Enigmas, through to 26 key Enigmas.

Figure 5. The reduced Enigma in its transparent box. Two wires are shown connected in the plugboard at the top of the machine, connecting A-S and E-T. The central silver object is the uniselector, which simulates the Enigma's rotors. In this photograph, 25 of its random connections can easily be seen, and the uniselector's 'rotor' is at the sixth position. The knobs and button at the bottom are used to change the initial key settings, as explained in the text. The reduced Enigma is 16«24«12cm.

Figure 6. Like the Swiss K Enigma, the reduced Eniigma has a remote lamp unit. Messages can be sent across a room to afford some privacy for the sender. The remote lamp unit can be used by people in the audience or videoed for projection (this allows the audience to see the code but not the plaintext).
Using the reduced Enigma
Each day the real Enigma's settings would be changed according to a code book. This was a complex procedure, designed to ensure that secure messages could be exchanged but that the enemy would be unlikely to read many messages using the same settings. Essentially, the operator chose a 'random' one-off setting, which was encoded on the Enigma using the code book's day setting. This brief code was then transmitted. The rotors were reset to the choice, and then the real message sent using that as the setting. In practice there were a number of other changes and code books used to further encrypt the message setting, and the details of the procedure changed throughout the war.
The code book for the reduced Enigma is much simpler than the real Enigma's, but can be used to show some of the cillies --- the likely human factors errors --- operators would make under wartime conditions.
To code: Choose any two letters from AEST: this will be the message setting. Set the reduced Enigma to the day settings, taken from the table in Appendix 2, and reset the Enigma. Code the two message setting letters and transmit using the day settings. Now set the Enigma to the message setting, reset it, and code the message to be sent. (This scheme is considerably simpler than the one used on the real Enigma, but it captures the spirit without unnecessary complication.)
To decode: Set the Enigma to the day settings, taken from the table. Decode the first two letters to obtain the message setting. Set the Enigma to the message setting, and reset it. Now decode the rest of the message as it arrives.
Because the reduced Enigma has knobs to set it, an operator may be tempted not to change its settings between messages. The simplest choice of letters for another message setting, then, is to repeat the initial settings. In contrast, on a real Enigma the rotors (and hence their settings) change position on each key press: thus on a real Enigma the easiest choice of message settings is to use is the final rotor position, not the initial, of a message.
When a second message is coded using predictable message settings it is of course easier to decode, and strict operational procedures were in place to help avoid it occurring. Bletchley Park called such procedural errors JABJABs, presumably because an early occurrence was the rotors set on JAB ending one message and 'reset' to JAB to start the next message.
There are many other sorts of cillies. For instance, were a message to end with the rotors set at HIT, the operator might find it hard to resist choosing the next message setting to be LER. The Army Enigma shown in Figures 1-3 used numeric settings, so there would be less of a temptation to use words.
The reduced Enigma does not have adjustable rotor rings as the real Enigma did during the war, and therefore they cannot be set from the code book. Thus the Herivel Tip cannot be demonstrated on the reduced Enigma. (Herivel suggested that operators, having rotated and set the rings on the rotors, might position the rotors in the easiest way, as it were just dropping them in to the Enigma, to obtain the message setting with no further rotations.)
Typical use in a lecture
Depending on the size of the audience or lecture room, it can help enormously to use a video camera and projector, so that people can easily seem the demonstrations. Before introducing the reduced Enigma, show some slides of the real Enigma and explain the major features.
The reduced Enigma is then demonstrated with the key length set to 1. The uniselector does not rotate, and the wiring does not change. It is then easy to explain the basic principles: no letter is coded as itself, and, by going through a simple example, the reciprocal nature of the code.
We then show how the code changes (pseudo) randomly when the uniselector is switched on. At this stage, it is best to have a key length of 50. It is easy to demonstrate that pressing a button repeatedly makes the lights come on unpredictably, and that it would be impossible (at least from such a short demonstration) to work out from which light was coming on which button had been pressed.
The setting mechanism can be explained: setting the two knobs and pressing the reset button can be done several times to confirm that the coding is repeatable.
The monthly code table is simple enough to be explained, and it helps that the date of the lecture can be used to select the initial settings.
The reduced Enigma can be used more easily without the complication of the message settting, a topic which can be introduced when the audience recognises the weakness of repeating messages (many times during a day) using fixed initial settings.
A volunteer resets the Enigma to the day settings, and selects a word (shown on the overhead projector) taken from Appendix 3 --- a list of words easily spelt with 4 letters. If the 'network' lamp box is used, another volunteer can write down the code directly. Otherwise two other volunteers are required: one to write down the code (and not reveal the word), who then acts as the 'transmitter' and takes the code over to the third volunteer.
A volunteer using the lamp board (on its 6m cable) can be far enough away not to see the other volunteer's button pressing. Alternatively the external lamp board can be projected using a video camera so the entire audience can see the code. But to decode the message, the reduced Enigma has to be brought over to the decoding volunteer. (External buttons on the lamp board would have simplified things, but would have made explaining what is going on more complex and less believable.)
It is surprisingly difficult to write down the coded message from the flashing lights; often there are requests to start again, and the sender will forget to reset the EnigmaÉ (There would typically be an Engima operator and an assistant.)
One persistent problem is that the volunteer coding often presses buttons almost as fast as they would as typing them --- forgetting that the other volunteer needs time to write down the code message. Typically, there are many opportunities to point out that all errors occur in a relatively calm lecture setting, which one can emphasise is a lot easier than being in a submarine at war!
The third volunteer is given the reduced Enigma, and types in the code. It is fun to do this first without resetting the Enigma: decoding will go wrong. When the Enigma is correctly set to the day settings, it will correctly decode the message (because of its reciprocal property).
After or during the demonstrations --- depending on audience participation --- it is helpful to emphasise that the encoding and decoding Enigmas must be both the same and initialised to the same settings. This observation leads into the key distribution problem, a topic which can be picked up in following lectures.
During the war, as the Germans worried about weaknesses in the Enigma code, they introduced further complications (such as more rotors). Because some boats and submarines would be at sea when the Enigmas were upgraded, the Germans were forced to transmit messages both on the old and new systems. This duplicate transmission often allowed Bletchley Park to work out the new Enigma wirings, and hence almost immediately compromise the "more secure" codes.
Cribs are easy to explain, since there are only a limited number of words that the reduced Enigma can work with (see Appendix 3). If volunteers can be pressed into coding longer messages, then it is possible to try to decode using a crib; however, finding the key settings requires a more detailed knowledge of the reduced Enigma than can be conveyed in a single lecture. Perhaps one day somebody will design a reduced Bombe good enough to be used real-time in lectures.
Some audiences worry about sending numbers: how can this be done with a plain alphabetic keyboard? Obviously, numbers could be spelt out, or a number code could be used. The Swiss K, which has 26 alphabetic letters, also labels ten letters 1 to 9. (Curiously, the letter O is labelled 9.) During the war, many numbers would have been map grid references: to reduce the chances of these important numbers being decoded, a special code book was used, which was changed from time to time. Thus grid references were transmitted as (coded) alphabetic words, rather than as latitude and longitude.
Some audiences may suggest that the 4 buttons might be labelled 00, 01, 10 and 11. Now any letter or digit can be coded using, say, ASCII or the older 5 bit (Baudot) code. One might then develop the discussion to introduce prefix free codes and other coding schemes.
Finally, one can introduce the concept of message setting, and explain how it increases security (because now the day setting is only used for a two letter code, which has no intrinsic meaning). Discussing the rigours of real use of message settings nicely introduce further human factors issues. For example because of the difficulty of setting Enigmas (imagine being under war-time conditions in the field) it was common practice to repeat a letter such as AAA or BBB at the beginning of a transmission so that the recipients could check the machine's day settings were correct.
More advanced topics
Lectures that go on to discuss public key cryptography will doubtlesss discuss trapdoor functions (see Bauer, 1997; or Singh, 2000, for a more popular account). One way to introduce these is to discuss the equivalent logic implementation of the reduced Enigma: decoding is then reduced to satisfiability. Satisfiability is NP hard, and a good example of a trapdoor function: given some variables and their values (e.g., in this case the binary representation of the message setting and the plaintext) one can very easily construct a particular Boolean formula that is true if and only if the variables have the given values. Decoding means finding the values of the variables from the formula, and this is much harder (though of course the reduced Enigma has some structure that might be exploited: even so, there is no fast way to decode in general).
In any lecture it is worth emphasising that the Enigma achieved its secrecy by trying to ensure that its physical construction was secure (specifically, trying to ensure it never fell into enemy hands): in contrast, we believe NP problems are hard because they are open to inspection. Of all the people who've tried, nobody has found any efficient solutions. The openness of abstract problems therefore paradoxically ensures their strength, quite the opposite of the physical Enigma situation. (There are problems harder than NP, but that's for another lecture.)
The reduced Enigma does have one problem with this sort of explanation. Discussion of complexity (e.g., to claim that the Enigma represents a trapdoor function) can require distinguishing linear (e.g., coding), polynomial and exponential (e.g., decoding) problems. Now, the reduced Enigma has 4 buttons, which can be represented as two bits because 22=4. Confusingly, it's also the case that 2+2=2«2=22=4. Unless care is taken, then, the audience won't believe that decoding is seriously harder than encoding, because they can see --- in this case --- that the complexities of the linear and exponential problems are of the same order!
Simulating Enigmas by computer
Simpler than building a reduced Enigma is to use a computer program to simulate one. There are many programs available to do this, including Russell Schwager's award-winning Java applet. A picture of an Enigma can be projected onto a screen, and the audience shown how the Enigma works.
There are at least four disadvantages to using a simulation.
One needs to ensure the computer, software and projector all work happily
together. This isn't always as easy as it seems when lecture theatres have
projectors with resolutions that one's computer is not happy with. Secondly,
the more realistic the simulation, the harder it is to understand exactly what
is going on. Of course, a simulator might be reprogrammed to provide both a
real Enigma and a reduced Enigma for comparison and discussion. Thirdly, one
might not want to pass an expensive and delicate laptop around a lecture
theatre so that people can use it easily. But, finally, the main disadvantage
is that a computer simulation does not engage audiences. It is too complex and
loses the principles for the details of successful computer interaction.
Conclusions
A real Enigma is a fascinating gadget, but is very complex. Even if one is available they are too valuable to use freely in lectures. A reduced Enigma --- the simplest possible coding machine that faithfully works like a real Enigma --- is a very successful lecturing aid, which allows hands-on use, and no special worries about damage. Its much simplified design allows the principles of the Enigma code to be explained much more easily. (Being able to lock the rotors and have short key lengths is also very helpful.)
Most lectures on cryptography cannot go very deeply into worked examples of coding, because of the time required. A working machine helps enormously, because it automates the tedium of coding and decoding. In practice, the reduced Enigma has been used to explain two important cryptology concepts, which are usually lost in the practical complexity of a real Enigma: the key distribution problem, to motivate the advantages of public key cryptography; secondly, the human factors weaknesses of the Enigma conventions (such as choosing message settings).
The design of the reduced Enigma puts some of the design flaws of the real Enigma in a new light, and makes them very obvious. In today's computerised binary world, it is obvious that a code machine that cannot work in binary must have problems. Had Scherbius or one of the other early inventors built a reduced Enigma prototype, perhaps they would have noticed the fundamental problems. Instead, as time went by the Enigma concept was made increasingly complex --- adding more rotors, adding a plugboard --- without addressing its basic limitations. Even the plugboard has problems, again which are obvious with the reduced Enigma.
The basic limitations of the Enigma are very apparent in the reduced Enigma. Because its calculations are easier, the reduced Enigma shows that some of the standard claims of the complexity of the Enigma and of the difficulty of breaking its codes are over-stated. If the Axis powers had recognised some of the Enigma's limitations they could have fixed them; the moral is that when designing systems, first design reduced ones to get the principles right. In various forms (e.g., get computer programs working correctly then optimise them), this is standard wisdom, but too often ignored!
For lecturers and teachers, the lesson is that building real things for ourselves, checking closely what people say by doing our own experiments --- perhaps making our own mistakes too! --- is the best way of really understanding and learning, and even of progressing a field. It is certainly the most enjoyable and best foundation for communicating a fascinating subject.
Further resources
Excellent written accounts of the Enigma are Simon Singh's popular book The Code Book (2000), and David Kahn's The Codebreakers (1996a) which is a standard reference. Mallman Showell's Enigma U-Boats (2000) has numerous illustrations, both of the Enigma and of the submarine war. A recent book, which provides a more balanced view of both the Allies and Axis use of codes is Stephen Budiansky's Battle of Wits (2000). A mathematician's introduction to the field is Freidrich Bauer's Decrypted Secrets (1997). A popular film Enigma based on a story by Robert Harris (1996) has been made, which uses the Enigma and Bletchley Park as the backdrop to a fictional detective story.
Any serious student of the Enigma and its history should visit Bletchley Park (see www.bletchleypark.org.uk) where many exhibits and resources are available. Tony Sale's Codes and Ciphers in the Second World War web site at www.codesandciphers.org.uk provides a great variety of authoritative and extensive material, and is highly recommended.
References
Friedrich Bauer, Decrypted Secrets, Springer, 1997.
Tim Bell, Harold Thimbleby, Mike Fellows, Ian Witten, Neil Koblitz & Matthew Powell, "Explaining Cryptographic Systems to the General Public," Journal of Computers & Education, 40(3):199-215, 2003.
Stephen Budiansky, Battle of Wits, Penguin Books, 2000.
Robert Harris, Enigma, Arrow Books, 1996.
David Kahn, The Codebreakers, Scribner, 1996a.
David Kahn, Seizing The Enigma, Arrow, 1996b.
Jak P. Mallman Showell, Enigma U-Boats, Ian Allan, 2000.
Russell Schwager, Java applet Enigma simulation,
http://www.ugrad.cs.jhu.edu/~russell/classes/enigma/
Simon Singh, The Code Book, Fourth Estate, 2000.
Acknowledgements
Gresham College supported the development of the reduced Enigma, which was first used at a Gresham public lecture. Harold Thimbleby is a Royal Society-Wolfson Research Merit Award Holder. Tony Sale, Frank Carter and Simon Singh provided helpful information about Enigmas; this jourmal's anonymous referees made extensive and insightful comments for which the author is grateful. Figures 1 to 3 are my photographs of Simon Singh's Army Enigma. Figure 4 is taken from Kahn, 1996b.
Appendix 1: Programming problems
The reduced Enigma project required the solution of several problems, which in themselves generate interesting programming problems:
¥ Which four different letters generate the most words? (I chose AEST, though AERT does more words but doesn't make such good ones; see Appendix 3.)
¥ Which rotors should be used, and what is the correct uniselector wiring to simulate the chosen two rotating rotors?
¥ What is a best (most secure) random sequence that should be used on the 34 uniselector positions left that are not simulating the two rotors?
¥ Finally, how would one build a Bombe simulator to attack the reduced Enigma?
Appendix 2: Settings from the reduced Enigma code book
Reduced Enigma Daily Key Settings:
January 2002
|
Date |
Plugboard |
Rotor settings |
|
1 |
A-E, S-T |
E-E |
|
2 |
A-E, S-T |
E-E |
|
3 |
A-S, E-T |
S-T |
|
4 |
A-S |
E-T |
|
5 |
A-E |
S-E |
|
6 |
S-T |
E-A |
|
7 |
A-T |
S-T |
|
8 |
A-E, S-T |
A-A |
|
9 |
A-S, E-T |
S-T |
|
10 |
NONE |
A-T |
|
11 |
E-T |
A-S |
|
12 |
A-T |
T-A |
|
13 |
A-S, E-T |
A-S |
|
14 |
A-S |
E-E |
|
15 |
A-S, E-T |
S-S |
|
16 |
A-E, S-T |
S-S |
|
17 |
A-S, E-T |
A-A |
|
18 |
E-S |
T-S |
|
19 |
NONE |
A-T |
|
20 |
S-T |
T-T |
|
21 |
A-S |
T-T |
|
22 |
E-T |
A-T |
|
23 |
A-T |
S-E |
|
24 |
A-S, E-T |
S-A |
|
25 |
E-S |
T-E |
|
26 |
E-S |
A-S |
|
27 |
A-T, E-S |
E-E |
|
28 |
A-T |
A-S |
|
29 |
E-T |
T-S |
|
30 |
A-T, E-S |
A-E |
|
31 |
A-S |
E-S |
The reduced Enigma plugboard settings are changed daily. The real Enigma plugboard was at first changed less often than daily, which was a security risk (though one that had to be weighed against the size and complexity of codebooks, and the practical difficulties of replugging). The plugboard connections were changed daily from the end of 1936; during WWII the plugboard settings were changed every 8 hours --- a delicate balance of security against the risk of wiring the Enigma incorrectly and possibly having to retransmit messages, which would be a grave error.
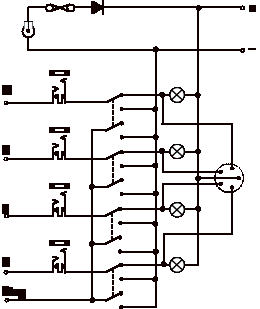


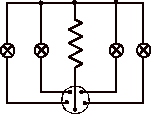
 Figure 12.
Figure 12.